|
Ski jump hydraulics |
|
Introduction |
|
Ski jumps in combination with plunge pools are widely used as an economic and effective type of energy dissipator downstream of large dams (Fig. 1). Ski jumps typically consist of an approach chute with a deflector at its end - the flip bucket - deflecting the discharge into the air. In this process, air is entrained into the jet reducing its scour potential during impact in the plunge pool. An inappropriate flip bucket design may result in a scour hole at the valley sides or close to the take-off section, endangering the stability of the valley sides or of the structure itself. An example includes the Nacimiento Dam, California, where a scour hole depth of tens of meters was observed after a flood in 1969. Despite hundreds of model studies conducted for specific prototypes, general guidelines were somehow incomplete when this research was launched in 2003. |

|
|

|
Personal research website of Dr Valentin Heller |
|
Circular-shaped flip bucket |
|
Fig. 1. Ski jump of Karakaya Dam, Turkey, in operation (journal title page to publication Heller et al. (2004), courtesy of Pöyry Infra AG, Switzerland)
|
|
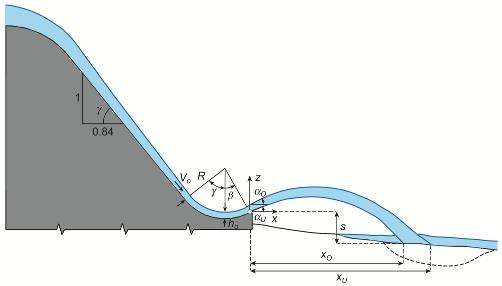
Fig. 2. Definition sketch for plane ski jump flow
|
|
Heller et al. (2005) investigated the ski jump hydraulics in a physical model. This research resulted in generic design criteria for the jet trajectories, pressures on the flip bucket, conditions of flow chocking (hydraulic jump) on flip bucket and energy dissipation as a function of the approach flow conditions (water depth ho, Froude number Fo) and the flip bucket geometry (angle b (beta) and radius R, Fig. 2).
|
|
Fig. 3. Ski jump model with deflection angle b (beta) = 30°, radius R = 0.40 m, approach flow water depth ho = 0.05 m and approach Froude number F = Vo/(gho)1/2 = 10 |
|
Triangular-shaped flip bucket |
|
A systematic investigation of a triangular-shaped flip bucket was investigated by a MSc student under Dr Heller’s co-supervision. A triangular-shaped flip bucket may be both cheaper and easier to construct than the conventional geometry. However, how does it perform from a hydraulic point of view? General guidelines for this alternative geometry were established in Steiner et al. (2008), including the jet trajectories, the pressure on the flip bucket and the conditions of flow chocking on the flip bucket (Fig. 4). As expected, peak pressures on the flip buckets are larger than for the circular-shaped geometry, however, the total force is smaller. No apparent disadvantage of this alternative flip bucket geometry was found. |
|
Selected publications |
|
Journals Heller, V., Pfister, M. (2009). Discussion of “Computing the trajectory of free jets” by Wahl, T.L., Frizell, K.H., Cohen, E.A. Journal of Hydraulic Engineering 135(7):622-623. Steiner, R., Heller, V., Hager, W.H., Minor, H.-E. (2008). Deflector ski jump hydraulics. Journal of Hydraulic Engineering 134(5):562-571 (http://dx.doi.org/10.1061/(ASCE)0733-9429(2008)134:5(562)). Heller, V., Hager, W.H., Minor, H.-E. (2006). Two Replies to Discussions of „Ski jump hydraulics“ by Khatsuria, R.M., and Novak, P. Journal of Hydraulic Engineering 132(10):1117. Heller, V., Hager, W.H., Minor, H.-E. (2005). Ski jump hydraulics. Journal of Hydraulic Engineering 131(5):347-354 (http://dx.doi.org/10.1061/(ASCE)0733-9429(2005)131:5(347)). Heller, V., Hager, W.H., Minor, H.-E. (2004). Skisprung – Allgemeine Bemessungsansätze. Wasser Energie Luft (7/8):183-187 (in German). Others Heller, V., Steiner, R. (2008). Skisprung - Eine alternative Deflektorgeometrie. Proc. Internationales Symposium Neue Anforderungen an den Wasserbau, VAW Mitteilung 207, 83-95, Minor, H.-E. ed. ETH Zurich, Zurich. Heller, V., Hager, W.H., Minor, H.-E. (2007). Hydraulics of ski jumps. Proc. 32nd IAHR Congress, Venice, Paper 377: 1-10, IAHR, Madrid. |




|
Fig. 4. Flow chocking observed on triangular-shaped flip bucket for decreasing discharge regime |
|
The jet trajectory can be described with mass point dynamics given by |
|
z(x) = zo + tanajx − gx2/(2Vo 2 cos2aj) |
|
In this equation x and z are the coordinates, aj (alpha) the take-off angle for the upper (O) or lower (U) jet trajectory and Vo is the approach flow velocity (Fig. 2). The parameter in this equation with the largest uncertainty is aj (alpha) which is not identical to the deflection angle b (beta) of the flip bucket. Effects such as jet disintegration and aerodynamic interactions result further in deviation between mass point dynamics and the observed jet throw distance XO or XU, respectively. |

|
Last modified: 24.04.2017 |
|
|